Digital frequency filter
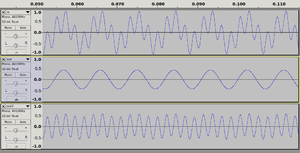
The following code uses a FIR (Finite Impulse Response) low-pass filter with a Hann window to split a signal into two components by a given frequency:
void split(const float in[], unsigned int n, float freq, float low[], float high[])
{
unsigned int window_n = sample_rate / freq;
float window[window_n];
float window_sum = 0.;
for (unsigned int i = 0; i < window_n; ++i) {
window[i] = .5 * (1. - cos(2. * i * M_PI / (window_n - 1)));
window_sum += window[i];
}
for (unsigned int i = 0; i < n; ++i) {
float sum = 0;
for (unsigned int j = 0; j < window_n; ++j) {
int index = i + j - window_n / 2;
if (index > 0 && index < n)
sum += in[index] * window[j];
}
low[i] = sum / window_sum;
high[i] = in[i] - low[i];
}
}
A property of this function is that you can recombine the low and high data using plain addition to recover the original input signal (modulo floating-point errors). This also makes it suitable for splitting a signal into multiple frequency bands; for example, calling it 7 times with different frequencies results in 8 output signals which can be independently gain-controlled and recombined.